Binary Tree Traversal

发表于 | 分类于

树的遍历

二叉树的遍历是算法问题中一个特别基础的问题，主要分为三种，前序，中序和后序，不同的遍历方法会将树的节点以不同的顺序输出，这篇文章主要用来记录二叉树三种遍历具体的代码实现。

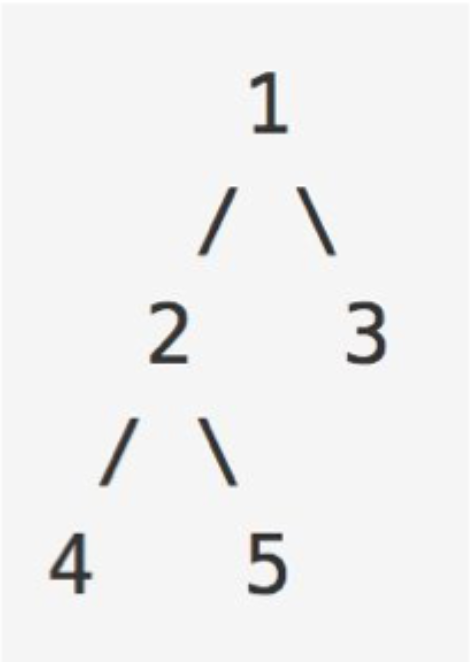
前序遍历: 1-245-3 (根 - 左 - 右)
中序遍历: 425-1-3 (左 - 根 - 右)
后序遍历: 452-3-1 (左 - 右 - 根)

二叉树的定义

要用代码实现二叉树的遍历，首先要用代码来定义一个二叉树，具体就是定义一个树的节点类 TreeNode 最基本的树的节点包括了值，左子树和右子树等属性，有一些更复杂的也会包含自己的父节点和左右的同辈节点等。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class TreeNode {
	TreeNode left, right;
	int value;
	
	TreeNode(int value) {
		this.value = value;
	}
	
	TreeNode(int value, TreeNode left, TreeNode right) {
		this.value = value;
		this.left = left;
		this.right = right;
	}
}

前序遍历

前序遍历是整个二叉树遍历中用非递归代码来实现相对比较容易的一种，其遍历顺序是先访问当前节点，再左子树节点，最后是右子树节点，所以顺序是: 跟 -> 左子节点 -> 右子节点，前序遍历其实就是DFS，具体的代码实现如下：

  • 递归实现
1
2
3
4
5
6
7
public void preorderTraversal(TreeNode node, List<Integer> nodes) {
	if(node != null) {
		nodes.add(node.value);
		preorderTraversal(node.left, nodes);
		preorderTraversal(node.right, nodes);
	}
}
  • 非递归实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public List<Integer> preorderTraversal(TreeNode node) {
	Stack<TreeNode> stack = new Stack<>();
	List<Integer> nodes = new ArrayList<>();
	stack.push(node);
	
	while(!stack.isEmpty()) {
		TreeNode curt = stack.pop();
		nodes.add(curt.value);
		
		if(curt.right != null)
			stack.push(curt.right);
			
		if(curt.left != null)
			stack.push(curt.left);
	}
	
	return nodes;
}

中序遍历

中序遍历的顺序是先遍历左子树节点，再遍历当前节点最后遍历右子树节点，所以顺序是: 左子节点 -> 根 -> 右子节点，在二叉搜索树中，因为左子树节点小于当前节点，而右子节点大于等于当前节点，所以中序遍历能够按照升序将树中的节点输出，具体的代码实现如下:

  • 递归实现
1
2
3
4
5
6
7
public void inorderTraversal(TreeNode, List<Integer> nodes) {
	if(node != null) {
		inorderTraversal(node.left, nodes);
		nodes.add(node.value);
		inorderTraversal(node.right, nodes);
	}
}
  • 非递归实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public void inorderTraversal(TreeNode node) {
	Stack<TreeNode> stack = new Stack<>();
	List<Integer> nodes = new ArrayList<>();
	TreeNode curt = node;
	
	while(curt != null || stack.isEmpty()) {
		while(curt != null) {
			stack.push(curt);
			curt = curt.left;
		}
		curt = stack.pop();
		nodes.add(curt.value);
		curt = curt.right;
	}
	return nodes;
}

后序遍历

后序遍历的顺序是先遍历左子节点，再遍历右子节点，最后遍历当前节点。所以顺序是: 左子节点 -> 右子节点 -> 根，具体代码实现如下:

  • 递归实现
1
2
3
4
5
6
7
public void postorderTraversal(TreeNode node, List<Integer> nodes) {
	if(node =! null) {
		postorderTraversal(node.left, nodes);
		postorderTraversal(node.right, nodes);
		nodes.add(node.value);
	}
}
  • 非递归实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public List<Integer> postorderTraversal(TreeNode node) {
	Stack<TreeNode> stack = new Stack<>();
	List<Integer> nodes = new ArrayList<>();
	TreeNode prev = null;
	
	stack.push(node);
	while(!stack.isEmpty()) {
		TreeNode curt = stack.peek();
		if(prev == null || prev.left == curt || prev.right == curt) {
			if(curt.left != null) 
				stack.push(curt.left);
			else if(curt.right != null)
				stack.push(curt.right);
		} else if(curt.left == prev) {
			if(curt.right != null)
				stack.push(curt.right);
		} else {
			nodes.add(curt.value);
			stack.pop();
		}
		prev = curt;
	}
	return nodes;
}